Test-prep Strategies for GMAT Data Sufficiency Problems
INTRODUCTION DATA SUFFICIENCY
Most people have much more difficulty with the Data Sufficiency problems
than with the Standard GMAT Math problems. However, the mathematical knowledge
and skill required to solve Data Sufficiency problems is no greater than
that required to solve standard math problems. What makes Data Sufficiency
problems appear harder at first is the complicated directions. But once
you become familiar with the directions, you'll find these problems no
harder than standard math problems. In fact, people usually become proficient
more quickly on Data Sufficiency problems.
If you like this material, you'll love the course!
GMAT Course Online

This interactive, comprehensive self-study course presents the
equivalent of over 600 pages of printed material, including hundreds of GMAT examples
and problems and feedback from GMAT experts to your questions.
In addition, the powerful learning engine StudyDesk increases your learning
efficiency by monitoring your progress and directing you to areas where you need further study. All for only $49.95!
Click the link above for a tour of the course.
Course Features:
Ask Questions! Our instructors monitor StudyDesk to answer your questions. StudyDesk also records the step where you make a mistake or ask a question. This is just one of many powerful educational tools in StudyDesk.
Highly Interactive You can take notes, view solutions, view reports, etc.
Versatile You can access the course from any computer at any time.
Statistics Your performance on the exercises is saved and you may review your performance and check solutions at any time. You can also check your ranking based on all students taking the course. How cool is that!
Guarantee If, at the end of the course, you do not feel sufficiently prepared for the test, you may repeat the course for free -- with full access to our instructors.
THE DIRECTIONS
The directions for GMAT Data Sufficiency questions are rather complicated.
Before reading any further, take some time to learn the directions cold.
Some of the wording in the directions below has been changed from the GMAT
to make it clearer. You should never have to look at the instructions during
the GMAT.
Directions: Each of the following Data Sufficiency problems contains
a question followed by two statements, numbered (1) and (2). You need not
solve the problem; rather you must decide whether the information given
is sufficient to solve the problem.
The correct answer to a question is
A if statement (1) ALONE is sufficient to answer the question
but statement (2) alone is not sufficient;
B if statement (2) ALONE is sufficient to answer the question
but statement (1) alone is not sufficient;
C if the two statements TAKEN TOGETHER are sufficient to answer
the question, but NEITHER statement ALONE is sufficient;
D if EACH statement ALONE is sufficient to answer the question;
E if the two statements TAKEN TOGETHER are still NOT sufficient
to answer the question.
Numbers: Only real numbers are used. That is, there are no complex numbers.
Drawings: The drawings are drawn to scale according to the information
given in the question, but may conflict with the information given in statements
(1) and (2).
You can assume that a line that appears straight is straight and that
angle measures cannot be zero.
You can assume that the relative positions of points, angles, and objects
are as shown.
All drawings lie in a plane unless stated otherwise.
Example:
| In triangle ABC to the right, what is the value of y?
(1) AB = AC
(2) x = 30 |
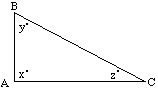 |
Explanation: By statement (1), triangle ABC is isosceles. Hence, its
base angles are equal: y = z. Since the angle sum of a triangle is 180
degrees, we get x + y + z = 180. Replacing z with y in this equation and
then simplifying yields x + 2y = 180. Since statement (1) does not give
a value for x, we cannot determine the value of y from statement (1) alone.
By statement (2), x = 30. Hence, x + y + z = 180 becomes 30 + y + z = 180,
or y + z = 150. Since statement (2) does not give a value for z, we cannot
determine the value of y from statement (2) alone. However, using both
statements in combination, we can find both x and z and therefore y. Hence,
the answer is C.
Notice in the above example that the triangle appears to be a right
triangle. However, that cannot be assumed: angle A may be 89 degrees or
91 degrees, we can't tell from the drawing. You must be very careful
not to assume any more than what is explicitly given in a Data Sufficiency
problem.
ELIMINATION
GMAT Data Sufficiency questions provide fertile ground for elimination. In
fact, it is rare that you won't be able to eliminate some answer-choices.
Remember, if you can eliminate at least one answer choice, the odds of
gaining points by guessing are in your favor.
The following table summarizes how elimination functions with Data Sufficiency
problems.
| Statement |
Choices Eliminated |
| (1) is sufficient |
B, C, E |
| (1) is not sufficient |
A, D |
| (2) is sufficient |
A, C, E |
| (2) is not sufficient |
B, D |
| (1) is not sufficient and (2) is not sufficient |
A, B, D |
Example 1: What is the 1st term in sequence S?
(1) The 3rd term of S is 4.
(2) The 2nd term of S is three times the 1st, and the 3rd term is four
times the 2nd.
(1) is no help in finding the first term of S. For example, the following
sequences each have 4 as their third term, yet they have different first
terms:
0, 2, 4
-4, 0, 4
This eliminates choices A and D. Now, even if we are unable to solve
this problem, we have significantly increased our chances of guessing correctly--from
1 in 5 to 1 in 3.
Turning to (2), we completely ignore the information in (1). Although
(2) contains a lot of information, it also is not sufficient. For example,
the following sequences each satisfy (2), yet they have different first
terms:
1, 3, 12
3, 9, 36
This eliminates B, and our chances of guessing correctly have increased
to 1 in 2.
Next, we consider (1) and (2) together. From (1), we know "the 3rd term
of S is 4." From (2), we know "the 3rd term is four times the 2nd." This
is equivalent to saying the 2nd term is 1/4 the 3rd term: (1/4)4 = 1. Further,
from (2), we know "the 2nd term is three times the 1st." This is equivalent
to saying the 1st term is 1/3 the 2nd term: (1/3)1 = 1/3. Hence, the first
term of the sequence is fully determined: 1/3, 1, 4. The answer is C.
| Example 2: In the figure to the right, what is the area of the
triangle?
(1)
(2) x = 90 |
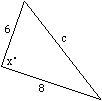 |
Recall that a triangle is a right triangle if and only if the square
of the longest side is equal to the sum of the squares of the shorter sides
(Pythagorean Theorem). Hence, (1) implies that the triangle is a right
triangle. So the area of the triangle is (6)(8)/2. Note, there is no need
to calculate the area--we just need to know that the area can be calculated.
Hence, the answer is either A or D.
Turning to (2), we see immediately that we have a right triangle. Hence,
again the area can be calculated. The answer is D.
Example 3: Is p < q ?
(1) p/3 < q/3
(2) -p + x > -q + x
Multiplying both sides of p/3 < q/3 by 3 yields p < q.
Hence, (1) is sufficient. As to (2), subtract x from both sides of -p
+ x > -q + x, which yields -p > -q.
Multiplying both sides of this inequality by -1, and recalling that
multiplying both sides of an inequality by a negative number reverses the
inequality, yields p < q.
Hence, (2) is also sufficient. The answer is D.
Example 4: If x is both the cube of an integer and between 2
and 200, what is the value of x?
(1) x is odd.
(2) x is the square of an integer.
Since x is both a cube and between 2 and 200, we are looking at the integers:

which reduce to
8, 27, 64, 125
Since there are two odd integers in this set, (1) is not sufficient
to uniquely determine the value of x. This eliminates choices A and D.
Next, there is only one perfect square, 64, in the set. Hence, (2) is
sufficient to determine the value of x. The answer is B.
Example 5: Is CAB a code word in language Q?
(1) ABC is the base word.
(2) If C immediately follows B, then C can be moved to the front of
the code word to generate another word.
From (1), we cannot determine whether CAB is a code word since (1) gives
no rule for generating another word from the base word. This eliminates
A and D.
Turning to (2), we still cannot determine whether CAB is a code word
since now we have no word to apply this rule to. This eliminates B.
However, if we consider (1) and (2) together, then we can determine
whether CAB is a code word:
From (1), ABC is a code word.
From (2), the C in the code word ABC can be moved to the front of the
word: CAB.
Hence, CAB is a code word and the answer is C.
UNWARRANTED ASSUMPTIONS
Be extra careful not to read any more into a statement than what is
given.
* The main purpose of some difficult problems on the GMAT is to lure you into making
an unwarranted assumption.
If you avoid the temptation, these problems can become routine.
Example 6: Did Incumbent I get over 50% of the vote?
(1) Challenger C got 49% of the vote.
(2) Incumbent I got 25,000 of the 100,000 votes cast.
If you did not make any unwarranted assumptions, you probably did not
find this to be a hard problem. What makes a problem difficult is not necessarily
its underlying complexity; rather a problem is classified as difficult
if many people miss it. A problem may be simple yet contain a psychological
trap that causes people to answer it incorrectly.
The above problem is difficult because many people subconsciously assume
that there are only two candidates. They then figure that since the challenger
received 49% of the vote the incumbent received 51% of the vote. This would
be a valid deduction if C were the only challenger (You might ask, "What
if some people voted for none-of-the-above?" But don't get carried away
with finding exceptions. The writers of the GMAT would not set a trap that
subtle). But we cannot assume that. There may be two or more challengers.
Hence, (1) is insufficient.
Now, consider (2) alone. Since Incumbent I received 25,000 of the 100,000
votes cast, I necessarily received 25% of the vote. Hence, the answer to
the question is "No, the incumbent did not receive over 50% of the vote."
Therefore, (2) is sufficient to answer the question. The answer is B.
Note, some people have trouble with (2) because they feel that the question
asks for a "yes" answer. But on Data Sufficiency questions, a "no" answer
is just as valid as a "yes" answer. What we're looking for is a definite
answer.
CHECKING EXTREME CASES
* When drawing a geometric figure or checking a given one, be sure to
include drawings of extreme cases as well as ordinary ones.
| Example 1: In the figure to the right, AC is a chord and B is
a point on the circle. What is the measure of angle x? |
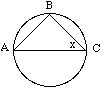 |
Although in the drawing AC looks to be a diameter, that cannot
be assumed. All we know is that AC is a chord. Hence, numerous cases
are possible, three of which are illustrated below:
In Case I, x is greater than 45 degrees; in Case II, x equals 45 degrees;
in Case III, x is less than 45 degrees. Hence, the given information is
not sufficient to answer the question.
Example 2: Three rays emanate from a common point and form three
angles with measures p, q, and r. What is the measure of q + r ?
It is natural to make the drawing symmetric as follows:
In this case, p = q = r = 120, so q + r = 240. However, there are
other drawings possible. For example:
In this case, q + r = 180. Hence, the given information is not sufficient
to answer the question.
Problems:
1. Suppose 3p + 4q = 11. Then what is the value of q?
(1) p is prime.
(2) q = -2p
(1) is insufficient. For example, if p = 3 and q = 1/2, then 3p + 4q
= 3(3) + 4(1/2) = 11. However, if p = 5 and q = -1, then 3p + 4q = 3(5)
+ 4(-1) = 11. Since the value of q is not unique, (1) is insufficient.
Turning to (2), we now have a system of two equations in two unknowns. Hence,
the system can be solved to determine the value of q. Thus, (2)
is sufficient, and the answer is B.
2. What is the perimeter of triangle ABC above?
(1) The ratio of DE to BF is 1: 3.
(2) D and E are midpoints of sides AB and CB, respectively.
Since we do not even know whether BF is an altitude, nothing can be
determined from (1). More importantly, there is no information telling
us the absolute size of the triangle.
As to (2), although from geometry we know that DE = AC/2, this relationship
holds for any size triangle. Hence, (2) is also insufficient.
Together, (1) and (2) are also insufficient since we still don't have
information about the size of the triangle, so we can't determine the perimeter.
The answer is E.
3. A dress was initially listed at a price that would have given the
store a profit of 20 percent of the wholesale cost. What was the wholesale
cost of the dress?
(1) After reducing the asking price by 10 percent, the dress sold for
a net profit of 10 dollars.
(2) The dress sold for 50 dollars.
Consider just the question setup. Since the store would have made a
profit of 20 percent on the wholesale cost, the original price P of the
dress was 120 percent of the cost: P = 1.2C. Now, translating (1) into
an equation yields:
P - .1P = C + 10
Simplifying gives
.9P = C + 10
Solving for P yields
P = (C + 10)/.9
Plugging this expression for P into P = 1.2C gives
(C + 10)/.9 = 1.2C
Since we now have only one equation involving the cost, we can determine
the cost by solving for C. Hence, the answer is A or D.
(2) is insufficient since it does not relate the selling price to any
other information. Note, the phrase "initially listed" implies that there
was more than one asking price. If it wasn't for that phrase, (2) would
be sufficient. The answer is A.
4. What is the value of the two-digit number x?
(1) The sum of its digits is 4.
(2) The difference of its digits is 4.
Considering (1) only, x must be 13, 22, 31, or 40. Hence, (1) is not
sufficient to determine the value of x.
Considering (2) only, x must be 40, 51, 15, 62, 26, 73, 37, 84, 48,
95, or 59. Hence, (2) is not sufficient to determine the value of x.
Considering (1) and (2) together, we see that 40 and only 40 is common
to the two sets of choices for x. Hence, x must be 40. Thus, together (1)
and (2) are sufficient to uniquely determine the value of x. The answer
is C.
5. If x and y do not equal 0, is x/y an integer?
(1) x is prime.
(2) y is even.
(1) is not sufficient since we don't know the value of y. Similarly,
(2) is not sufficient. Furthermore, (1) and (2) together are still insufficient
since there is an even prime number--2. For example, let x be the prime
number 2, and let y be the even number 2 (don't forget that different variables
can stand for the same number). Then x/y = 2/2 = 1, which is an integer.
For all other values of x and y, x/y is not an integer. (Plug in a few
values to verify this.) The answer is E.
6. Is 500 the average (arithmetic mean) score on the GMAT?
(1) Half of the people who take the GMAT score above 500 and half of
the people score below 500.
(2) The highest GMAT score is 800 and the lowest score is 200.
Many students mistakenly think that (1) implies the average is 500.
Suppose just 2 people take the test and one scores 700 (above 500) and
the other scores 400 (below 500). Clearly, the average score for the two
test-takers is not 500. (2) is less tempting. Knowing the highest and lowest
scores tells us nothing about the other scores. Finally, (1) and (2) together
do not determine the average since together they still don't tell us the
distribution of most of the scores. The answer is E.
7. The set S of numbers has the following properties:
I) If x is in S, then 1/x is in S.
II) If both x and y are in S, then so is x + y.
Is 3 in S?
(1) 1/3 is in S.
(2) 1 is in S.
Consider (1) alone. Since 1/3 is in S, we know from Property I that
1/(1/3) = 3 is in S. Hence, (1) is sufficient.
Consider (2) alone. Since 1 is in S, we know from Property II that 1 + 1 =
2 (Note, nothing in Property II prevents x and y from standing for
the same number. In this case both stand for 1.) is in S. Applying
Property II again shows that 1 + 2 = 3 is in S. Hence, (2) is also
sufficient. The answer is D.
8. What is the area of the triangle above?
(1) a = x, b = 2x, and c = 3x.
(2) The side opposite a is 4 and the side opposite b is 3.
From (1) we can determine the measures of the angles: a + b + c = x
+ 2x + 3x = 6x = 180
Dividing the last equation by 6 gives: x = 30
Hence, a = 30, b = 60, and c = 90. However, different size triangles can have
these angle measures, as the diagram below illustrates:
Hence, (1) is not sufficient to determine the area of the triangle.
Turning to (2), be careful not to assume that c is a right angle. Although
from the diagram c appears to be a right angle, it could be 91 degrees
or 89 degrees--we can't tell. Hence, (2) is not sufficient to determine
the area of the triangle.
However, with both (1) and (2), c is a right angle and the area
of the triangle is (1/2)(base)(height) = (1/2)(4)(3). The answer
is C.
|

