Diagnostic Test - Games - Logical Connectives - Review

Click the links immediately below to view the other diagnostic tests.

Reading Test     Arguments Test

LOGICAL CONNECTIVES
While no training in formal logic is required for the LSAT, essentially it is a logic test. So some knowledge of formal logic will give you a definite advantage.

To begin, consider the seemingly innocuous connective "if..., then...." Its meaning has perplexed both the philosopher and the layman through the ages. The statement "if A, then B" means by definition "if A is true, then B must be true as well," and nothing more. For example, we know from experience that if it is raining, then it is cloudy. So if we see rain falling past the window, we can validly conclude that it is cloudy outside.

There are three statements that can be derived from the implication "if A, then B"; two are invalid, and one is valid.

From "if A, then B" you cannot conclude "if B, then A." For example, if it is cloudy, you cannot conclude that it is raining. From experience, this example is obviously true; it seems silly that anyone could commit such an error. However, when the implication is unfamiliar to us, this fallacy can be tempting.

Another, and not as obvious, fallacy derived from "if A, then B" is to conclude "if not A, then not B." Again, consider the weather example. If it is not raining, you cannot conclude that it is not cloudy--it may still be overcast. This fallacy is popular with students.

Finally, there is one statement that is logically equivalent to "if A, then B." Namely, "if not B, then not A." This is called the contrapositive, and it is very important.

If there is a key to performing well on the LSAT, it is the contrapositive.

To show the contrapositive's validity, we once again appeal to our weather example. If it is not cloudy, then from experience we know that it cannot possibly be raining.

We now know two things about the implication "if A, then B":

1) If A is true, then B must be true.
2) If B is false, then A must be false.

If you assume no more that these two facts about an implication, then you will not fall for the fallacies that trap many students.

We often need to rephrase a statement when it's worded in a way that obscures the information it contains.

On the LSAT, as in everyday speech, two negatives make a positive--they cancel each other out.

not(not A) = A

Example:
"It is not the case that John did not pass the LSAT" means the same thing as "John did pass the LSAT."

The statement "if A, then B; and if B, then A" is logically equivalent to "A if and only if B." Think of "if and only if" as an equal sign: if one side is true, then the other side must be true, and if one side is false, then the other side must be false.

(If A, then B; and if B, then A) = (A if and only if B)

 

A if and only if B
A	B
True	True
False	False

Example:
"If it is sunny, then Biff is at the beach; and if Biff is at the beach, then it is sunny" is logically equivalent to "It is sunny if and only if Biff is at the beach."

"A only if B" means that when A occurs, B must also occur. That is, "if A, then B."

A only if B = if A, then B

Example:
"John will do well on the LSAT only if he studies hard" is logically equivalent to "If John did well on the LSAT, then he studied hard."

(Note: Students often wrongly interpret this statement to mean "if John studies hard, then he will do well on the LSAT." There is no such guarantee. The only guarantee is that if he does not study hard, then he will not do well.)

The statement "A unless B" means that A is true in all cases, except when B is true. In other words if B is false, then A must be true. That is, if not B, then A.

A unless B = if not B, then A

Example:
"John did well on the LSAT unless he partied the night before"

is logically equivalent to

"If John did not party the night before, then he did well on the LSAT."

The two statements "if A, then B" and "if B, then C" can be combined to give "if A, then C." This is called the transitive property.

("If A, then B" and "if B, then C") = ("if A, then C")

Example:
From the two statements "if John did well on the LSAT, then he studied hard" and "if John studied hard, then he did not party the night before the test" you can conclude that "if John did well on the LSAT, then he did not party the night before the test."

DIAGRAMMING
Virtually every game can be solved more easily and efficiently by using a diagram. Unless you have a remarkable memory and can process reams of information in your head, you must draw a diagram. Because of the effectiveness of diagrams, games are the best candidates for improvement. A well-constructed diagram can change a convoluted, unwieldy mass of information into an easily read list. In fact, from a well-constructed diagram, you can often read-off the answers without any additional thought.

Symbols
The ability to symbolize sentences is one of the most important skills you need to develop for the LSAT.

Five basic symbols are used throughout this discussion. They are

Symbol	Meaning
&	and
or	or
~	not
-->	If..., then...
( )	parentheses

ORDERING GAMES
Ordering games are the easiest games, and fortunately they also appear the most often.

Line-up Game
There are five people--Bugsy, Nelson, Dutch, Clyde, and Gotti--in a police line-up standing in spaces numbered 1 through 6, from left to right. The following conditions apply:

There is always one empty space.
Clyde is not standing in space 1, 3, or 5.
Gotti is the third person from the left.
Bugsy is standing to the immediate left of Nelson.

"Clyde is not standing in space 1, 3, or 5" is symbolized as C = not(1,3,5). "Gotti is the third person from the left" is naturally symbolized as G = 3rd. Note: the fact that Gotti is third does not force him into space 3--he could stand in spaces 3 or 4. "Bugsy is standing to the immediate left of Nelson" is symbolized as BN. The diagram will consist of 6 dashes:

_1_ _2_ _3_ _4_ _5_ _6_

When placing the elements on the diagram, first look for a condition that fixes the position of an element. There is none. Next, we look for a condition that limits the position of an element. The second condition, "Gotti is the third person from the left," limits Gotti to spaces 3 and 4. This condition, as often happens with ordering games, generates two diagrams: one with the empty space to Gotti's left and one with the empty space to his right:

Diagram I ___ ___ ___ _G_ ___ ___

Diagram II ___ ___ _G_ ___ ___ ___

Next, we look for a condition that connects two or more people. The last condition, BN, connects B with N. However, at this stage we cannot place it on the diagram. Finally, we look for a condition that states where a person cannot be standing. The first condition states that Clyde cannot be standing in space 1, 3, or 5. Noting this on the diagram yields

Diagram I _~C_ ___ _~C_ _G_ _~C_ ___

Diagram II _~C_ ___ _G_ ___ _~C_ ___

(Note: D is "wild" because the conditions do not refer to him. Thus D can stand in more positions than any other person.)

This diagram is self-contained. There is no need to refer to the original problem. If possible, avoid rereading the problem.

1. Nelson CANNOT stand in which one of the following spaces?

(A) 2 (B) 3 (C) 4 (D) 5 (E) 6

The method of solution to this problem is rather mechanical: We merely place Nelson in one of the spaces offered. Then check whether it is possible to place the other people in the line-up without violating any initial condition. If so, then we eliminate that answer-choice. Then place Nelson in another space offered, and repeat the process.

To that end, place Nelson in space 2 in Diagram II:

_~C_ _N_ _G_ ___ _~C_ ___

From the condition BN, we know that B must be in space 1:

_B_ _N_ _G_ ___ _~C_ ___

Now D could stand in space 4, and C could stand in space 6--both without violating any initial condition:

_B_ _N_ _G_ _D_ _X_ _C_ (Where X means "empty.")

This diagram is consistent with the initial conditions. So N could stand in space 2. This eliminates choice (A).

Next, place Nelson in space 4. Then Diagram I is violated since G is already in space 4, and Diagram II is also violated since there is no room for the condition BN:

The answer is (C).

2. Which one of the following spaces CANNOT be empty?

(A) 1 (B) 2 (C) 3 (D) 4 (E) 5

Assume that space 1 is empty. Then in Diagram I, the condition BN can be placed in spaces 2 and 3, D can be placed in space 5, and C can be placed in space 6--all without violating any initial condition:

_X_ _B_ _N_ _G_ _D_ _C_

Thus space 1 could be empty. This eliminates (A).

Next, assume that space 2 is empty. In Diagram I, this forces BN into spaces 5 and 6:

___ _X_ ___ _G_ _B_ _N_

However, this diagram does not leave room for C [recall C = not(1, 3, 5)]. Diagram I is thus impossible when space 2 is empty. Turning to Diagram II, we see immediately that space 2 cannot be empty, for this would make G second, violating the condition G = 3rd. Hence Diagram II is also impossible when space 2 is empty.

Thus space 2 cannot be empty, and the answer is (B).

GROUPING GAMES
Because grouping games partition elements into sets, the number of elements is often an issue. Counting may have been one of man's first thought processes; nevertheless, counting possibilities is deceptively hard. This tends to make grouping games more difficult than ordering games. Pay close attention to the maximum or minimum number of elements in a group; this is often the heart of the game.

Selection Game
The starting line-up for the Olympic basketball "Dream Team" is chosen from the following two groups:

Group A: Johnson, Drexler, Bird, Ewing
Group B: Laettner, Robinson, Jordan, Malone, Pippen

The following requirements must be meet:
Two players are chosen from Group A, and three from Group B.
Jordan starts only if Bird starts.
Drexler and Bird do not both start.
If Jordan starts, then Malone does not.
Exactly 3 of the four fast-break specialists--Johnson, Bird, Jordan, Pippen--must be chosen.

It is best to solve this problem without a diagram; however, we will still symbolize the conditions for clarity and easy reference. The condition "Jordan starts only if Bird starts" implies only that if Jordan is starting then Bird must be starting as well. So we symbolize it as Jordan->Bird. The condition "Drexler and Bird do not both start" means that if one starts then the other does not. So we symbolize it as Drexler->~Bird. Students often misinterpret this condition to mean that neither of them starts. To state that neither starts, put both at the beginning of the sentence: Both Drexler and Bird do not start.

The condition "If Jordan starts, then Malone does not" is naturally symbolized as Jordan->~Malone. It tells us that if J starts then M does not, but tells us nothing when M does not start. Such a condition, where the two parts of an if-then statement do not similarly affect each other, is called a nonreciprocal condition. On the other hand, a condition such as Jordan<->~Malone affects J and M equally. In this case, we are told that if J starts then M does not as before, but we are told additionally that if M does not start then J does. It is important to keep the distinction between reciprocal and nonreciprocal relations clear; a common mistake is to interpret a nonreciprocal relation as reciprocal. The remaining conditions cannot be easily written in symbol form, but we will paraphrase them in the schematic:

Jordan->Bird
Drexler->~Bird
Jordan->~Malone
2 from Group A
3 from Group B
fast-break specialists: Johnson, Bird, Jordan, Pippen
3 fast-break specialists
Ewing, Laettner, Robinson are "wild"

Note: Ewing, Laettner, and Robinson are independent because there are no conditions that refer directly to them. We now turn to the questions.

1. If Jordan starts, which of the following must also start?
(A) Malone or Johnson
(B) Drexler or Laettner
(C) Drexler or Johnson
(D) Johnson or Pippen
(E) Malone or Robinson

From the condition Jordan->Bird, we know that if Jordan starts, then Bird must start as well. Now both Jordan and Bird are fast-break specialists, and three of the four fast-break specialists must start. So at least one of the remaining fast-break specialists--Johnson or Pippen--must also start. The answer is (D).

2. All of the following pairs of players can start together EXCEPT:
(A) Ewing and Drexler
(B) Jordan and Johnson
(C) Robinson and Johnson
(D) Johnson and Bird
(E) Pippen and Malone

Begin with choice (A). Both Ewing and Drexler are from Group A, so the remaining 3 starters must be chosen from Group B. Additionally, they must all be fast-break specialists since neither E nor D is--there are exactly 3 fast-break specialists. But Jordan and Pippen are the only fast-break specialists in Group B. So the third fast-break specialist cannot be chosen. The answer therefore is (A). This type of question can be time consuming because you may have to check all the answer-choices--save these questions for last.

3. If Malone starts, which one of the following is a complete and accurate list of the players from Group A any one of whom could also start?
(A) J (B) J, D (C) J, B (D) J, D, B (E) J, E, B

Jordan cannot start with Malone according to the condition Jordan->~Malone. To play three fast-break specialists, therefore, Johnson, Bird, and Pippen are all required to start. Since both Johnson and Bird are from Group A and exactly two players from that group start, these two players comprise the complete list of starters from Group A when Malone also starts. The answer is (C).

4. Which one of the following players must start?
(A) Pippen (B) Johnson (C) Jordan (D) Malone (E) Bird

Suppose Bird does not start. Then the 3 fast-break specialists must be Johnson, Jordan, and Pippen. But if Jordan starts, then from the initial conditions Bird must also start. Hence Bird must always start. The answer is (E).

ASSIGNMENT GAMES
Assignment games match a characteristic with an element of the game. For example, you may be asked to assign a schedule: Bob works only Monday, Tuesday, or Friday. Or you may be told that a person is either a Democrat or a Republican.

Because the characteristics are typically assigned to groups of elements, assignment games can look very similar to grouping games. Additionally, in grouping games the groups are often identified by their characteristics. However, in assignment games you pair each element with one or more characteristics, whereas in grouping games you partition the elements into two or more groups.

Many assignment games can be solved very efficiently by using an elimination grid. An example will illustrate this method of diagramming.

Elimination Grid
Dean Peterson, Head of the Math Department at Peabody Polytech, is making the fall teaching schedule. Besides himself there are four other professors--Warren, Novak, Dornan, and Emerson. Their availability is subject to the following constraints.

Warren cannot teach on Monday or Thursday.
Dornan cannot teach on Wednesday.
Emerson cannot teach on Monday or Friday.
Associate Professor Novak can teach at any time.
Dean Peterson cannot teach evening classes.
Warren can teach only evening classes.
Dean Peterson cannot teach on Wednesday if Novak teaches on Thursday, and Novak teaches on Thursday if Dean Peterson cannot teach on Wednesday.
At any given time there are always three classes being taught.

We indicate that a teacher does not work at a particular time by placing an X on the elimination grid. Placing the conditions on a grid yields

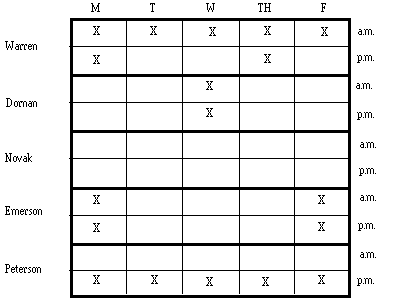
To answer the following questions, we will refer only to the table, not the original problem.

1. At which one of the following times can Warren, Dornan, and Emerson all be teaching?

(A) Monday morning
(B) Friday evening
(C) Tuesday evening
(D) Friday morning
(E) Wednesday morning

The table clearly shows that all three can work on Tuesday night. The answer is (C).

2. For which day will the dean have to hire a part-time teacher?

(A) Monday
(B) Tuesday
(C) Wednesday
(D) Thursday
(E) Friday

Dornan and Novak are the only people who can work Monday evenings, and three classes are always in session, so extra help will be needed for Monday evenings. The answer is (A).

3. Which one of the following must be false?

(A) Dornan does not work on Tuesday.
(B) Emerson does not work on Tuesday morning.
(C) Peterson works every day of the week except Wednesday.
(D) Novak works every day of the week except Wednesday.
(E) Dornan works every day of the week except Wednesday.

The condition "Dean Peterson cannot teach on Wednesday if Novak teaches on Thursday, and Novak teaches on Thursday if Dean Peterson cannot teach on Wednesday" can be symbolized as (P not W)<-->(N = TH). Now, if Novak works every day of the week, except Wednesday, then in particular he works Thursday. So from the condition (P not W)<-->(N = TH), we know that Dean Peterson cannot work on Wednesday. But from the table this leaves only Novak and Emerson to teach the three Wednesday morning classes. Hence the answer is (D).

4. If Novak does not work on Thursday, then which one of the following must be true?

(A) Peterson works Tuesday morning.
(B) Dornan works Tuesday morning.
(C) Emerson works on Tuesday.
(D) Peterson works on Wednesday.
(E) Warren works on Tuesday morning.

If you remember to think of an if-and-only-if statement as an equality, then this will be an easy problem. Negating both sides of the condition (P not W)<-->(N = TH) gives (P = W)<-->(N not TH). This tells us that Dean Peterson must work on Wednesday if Novak does not work on Thursday. The answer, therefore, is (D).

Caution: Not all scheduling games lend themselves to an elimination grid. It's sweet when this method can be applied because the answers typically can be read directly from the table with little thought. Only one-third of the assignment games, however, can be solved this way. Most often the game will require a more functional diagram, and you will need to spend more time tinkering with it.

When you first read an assignment game, you need to quickly decide whether or not to use an elimination grid. You may decide to use a table. Then spend three minutes trying to set it up, only to realize you have taken the wrong path and have wasted three minutes. Unfortunately, exact criteria cannot be given for when to use an elimination grid. But this much can be said: if only two options (characteristics) are available to the elements--yes/no, on/off, etc.--then an elimination grid is probably indicated.