The Math sections include two types of questions: Multiple-choice and Grid-ins.
They are designed to test your ability to solve problems, not to test your mathematical knowledge.
The questions in each sub-section are listed in ascending order of difficulty.
So, if a section begins with 8 multiple-choice questions followed by 10 grid-ins,
then Question 1 will be the easiest multiple-choice question and Question 8 will be the hardest.
Then Question 9 will be the easiest grid-in question and Question 18 will be the hardest.
There will be two 25-minute math sections and one 20-minute section. The sections can appear
anywhere in the test.
The mathematical skills tested on the SAT are very basic: only first
year algebra, geometry (no proofs), and a few basic concepts from second year algebra.
However, this does not mean that the math section is easy. The medium of basic mathematics is
chosen so that everyone taking the SAT will be on a fairly even playing
field. This way students who are concentrating in math and science
don't have an undue advantage over students who are concentrating in English
and humanities. Although the questions require only basic mathematics
and all have simple solutions, it can require considerable ingenuity to
find the simple solution. If you have taken a course in calculus
or another advanced math course, don't assume that you will find the math
section easy. Other than increasing your mathematical maturity, little
you learned in calculus will help on the SAT.
As mentioned above, every SAT math problem has a simple solution, but
finding that simple solution may not be easy. The intent of the math
section is to test how skilled you are at finding the simple solutions.
The premise is that if you spend a lot of time working out long solutions
you will not finish as much of the test as students who spot the short,
simple solutions. So if you find yourself performing long calculations
or applying advanced mathematics--stop. You're heading in the wrong
direction.
Tackle the math problems in the order given, and don't worry if you
fail to reach the last few questions. It's better to work accurately
than quickly.
You may bring a calculator to the test, but all questions can be answered
without using a calculator. Be careful not to overuse the calculator; it can slow you down.
Substitution is a very useful technique for solving SAT math problems.
It often reduces hard problems to routine ones. In the substitution
method, we choose numbers that have the properties given in the problem
and plug them into the answer-choices.
We are told that n is an odd integer. So choose an odd integer for n,
say, 1 and substitute it into each answer-choice. In Choice (A), 3(1) +
2 = 5, which is not an even integer. So eliminate (A). Next, n/4 = 1/4
is not an even integer--eliminate (B). Next, 2n + 3 = 2(1) + 3 = 5 is not
an even integer--eliminate (C). Next, n(n + 3) = 1(1 + 3) = 4 is even and
hence the answer is possibly (D). Finally, in Choice (E), the nn = 1(1)
= 1, which is not even--eliminate (E). The answer is (D).
When using the substitution method, be sure to check every answer-choice
because the number you choose may work for more than one answer-choice.
If this does occur, then choose another number and plug it in, and so on,
until you have eliminated all but the answer. This may sound like a lot
of computing, but the calculations can usually be done in a few seconds.
Sometimes instead of making up numbers to substitute into the problem,
we can use the actual answer-choices. This is called Plugging In. It is
a very effective technique but not as common as Substitution.
First, check to see which of the answer-choices has a sum of digits
equal to 18. For choice (A), 2 + 4 + 6 = 12. Eliminate. For choice (B),
3 + 6 + 9 = 18. This may be the answer. For choice (C), 5 + 3 + 1 = 9.
Eliminate. For choice (D), 8 + 5 + 5 = 18. This too may be the answer.
For choice (E), 8 + 9 + 3 = 20. Eliminate. Now, in choice (D), the ten's
digit is not twice the hundred's digit, 5 does not equal 2(8). Eliminate.
Hence, by process of elimination, the answer is (B). Note that we did not
need the fact that the hundred's digit is 1/3 the unit's digit.
Defined functions are very common on the SAT, and most students struggle
with them. Yet once you get used to them, defined functions can be some
of the easiest problems on the SAT. In this type of problem, you will
be given a symbol and a property that defines the symbol.
From the above definition, we know that x # y = xy - y. So all we have
to do is replace x with 2 and y with 3 in the definition: 2 # 3 = 2(3)
- 3 = 3. Hence, the answer is (B).
This broad category is a popular source for SAT questions. At first,
students often struggle with these problems since they have forgotten many
of the basic properties of arithmetic. So before we begin solving these
problems, let's review some of these basic properties.
The absolute value of a number, | |, is always positive. In other
words, the absolute value symbol eliminates negative signs.
For example, | -7 | = 7. Caution, the absolute value symbol acts only
on what is inside the symbol, | |. For example, -| -7 | = -(+7) = -7. Here,
only the negative sign inside the absolute value symbol is eliminated.
Example: If a, b, and c are consecutive integers and a < b
< c, which of the following must be true?
I. b - c = 1
II. abc/3 is an integer.
III. a + b + c is even.
(A) I only (B) II only (C) III only (D) I and II only (E) II and III
only
Let x, x + 1, x + 2 stand for the consecutive integers a, b, and c,
in that order. Plugging this into Statement I yields b - c = (x + 1) -
(x + 2) = -1. Hence, Statement I is false.
As to Statement II, since a, b, and c are three consecutive integers,
one of them must be divisible by 3. Hence, abc/3 is an integer, and Statement
II is true.
As to Statement III, suppose a is even, b is odd, and c is even. Then
a + b is odd since even + odd = odd. Hence, a + b + c = (a + b) + c = (odd)
+ even = odd. Thus, Statement III is not necessarily true. The answer is
(B).
GEOMETRY
One-fourth of the math problems on the SAT involve geometry.
(There are no proofs.) Fortunately, the figures on the SAT are
usually drawn to scale. Hence, you can check your work and in
some cases even solve a problem by "eyeballing" the drawing.
Following are some of the basic properties of geometry. You probably
know many of them. Memorize any that you do not know.
1. There are 180 degrees in a straight angle.
2. Two angles are supplementary if their angle sum is 180 degrees.
3. Two angles are complementary if their angle sum is 90 degrees.
4. Perpendicular lines meet at right angles.
5. A triangle with two equal sides is called isosceles. The angles
opposite the equal sides are called the base angles.
6. The altitude to the base of an isosceles or equilateral triangle
bisects the base and bisects the vertex angle.
7. The angle sum of a triangle is 180 degrees.
8. In an equilateral triangle all three sides are equal, and
each angle is 60 degrees.
9. The area of a triangle is bh/2, where b is the base and h
is the height.
10. In a triangle, the longer side is opposite the larger angle,
and vice versa.
11. Two triangles are similar (same shape and usually different
size) if their corresponding angles are equal. If two triangles
are similar, their corresponding sides are proportional.
12. Two triangles are congruent (identical) if they have the
same size and shape.
13. In a triangle, an exterior angle is equal to the sum of its
remote interior angles and is therefore greater than either of
them.
14. Opposite sides of a parallelogram are both parallel and congruent.
15. The diagonals of a parallelogram bisect each other.
16. If w is the width and l is the length of a rectangle, then
its area is A = lw and its perimeter is P=2w + 2l.
17. The volume of a rectangular solid (a box) is the product
of the length, width, and height. The surface area is the sum
of the area of the six faces.
18. If the length, width, and height of a rectangular solid (a
box) are the same, it is a cube. Its volume is the cube of one
of its sides, and its surface area is the sum of the areas of
the six faces.
19. A tangent line to a circle intersects the circle at only
one point. The radius of the circle is perpendicular to the tangent
line at the point of tangency.
20. An angle inscribed in a semicircle is a right angle.
| Example: In the figure to the right, what is the
value of x?
(A) 30 (B) 32 (C) 35 (D) 40 (E) 47 |
 |
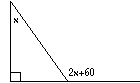Since 2x + 60 is an exterior angle, it is equal to the sum of
the remote interior angles. That is, 2x + 60 = x + 90. Solving
for x gives x = 30. The answer is (A).
Most geometry problems on the SAT require straightforward calculations.
However, some problems measure your insight into the basic rules
of geometry. For this type of problem, you should step back and
take a "birds-eye" view of the problem. The following example
will illustrate.
| Example: In the figure to the right, O is both
the center of the circle with radius 2 and a vertex of the
square OPRS. What is the length of diagonal PS?
(A) 1/2 (B) 1 (C) 4 (D) 2 (E) 2/3 |
 |
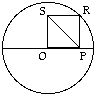The diagonals of a square are equal. Hence, line segment OR (not
shown) is equal to SP. Now, OR is a radius of the circle and therefore
OR = 2. Hence, SP = 2 as well, and the answer is (D).
COORDINATE GEOMETRY
Distance Formula:
The distance between points (x, y) and (a, b) is given by the
following formula:
| Example: In the figure to the right, the circle is centered
at the origin and passes through point P. Which of the following
points does it also pass through?
(A) (3, 3)
(B)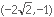
(C) (2, 6)
(D) (1.5, 1.3)
(E) (-3, 4) |
 |
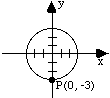Since the circle is centered at the origin and passes through
the point (0,-3), the radius of the circle is 3. Now, if any other
point is on the circle, the distance from that point to the center
of the circle (the radius) must also be 3. Look at choice (B).
Using the distance formula to calculate the distance between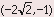
and (0, 0) (the origin) yields
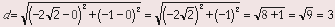
Hence,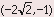 is
on the circle, and the answer is (B).
Midpoint Formula:
The midpoint M between points (x, y) and (a, b) is given by
M = ([x + a]/2, [y + b]/2)
In other words, to find the midpoint, simply average the corresponding
coordinates of the two points.
| Example: In the figure to the right, polygon PQRO
is a square and T is the midpoint of side QR. What are the
coordinates of T ?
(A) (1, 1) (B) (1, 2) (C) (1.5, 1.5) (D) (2, 1) (E) (2,
3) |
 |
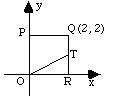Since point R is on the x-axis, its y-coordinate is 0. Further,
since PQRO is a square and the x-coordinate of Q is 2, the x-coordinate
of R is also 2. Since T is the midpoint of side QR, the midpoint
formula yields T = ([2 + 2]/2, [2 + 0]/2) = (4/2, 2/2) = (2, 1).
The answer is (D).
Slope Formula:
The slope of a line measures the inclination of the line. By
definition, it is the ratio of the vertical change to the horizontal
change. The vertical change is called the rise, and the horizontal
change is called the run. Thus, the slope is the rise over the
run. Given the two points (x, y) and (a, b) the slope is
M = (y - b)/(x - a)
| Example: In the figure to the right, what is the
slope of line passing through the two points?
(A) 1/4 (B) 1 (C) 1/2 (D) 3/2 (E) 2 |
 |
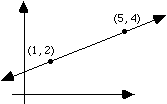The slope formula yields m = (4 - 2)/(5 - 1) = 2/4 = 1/2. The
answer is (C).
Slope-Intercept Form:
Multiplying both sides of the equation m = (y -b)/(x - a) by
x-a yields
y - b = m(x - a)
Now, if the line passes through the y-axis at (0, b), then the
equation becomes
y - b = m(x - 0)
y - b = mx
y = mx + b
This is called the slope-intercept form of the equation of a
line, where m is the slope and b is the y-intercept. This form
is convenient because it displays the two most important bits
of information about a line: its slope and its y-intercept.
Example: The equation of the line above is y = 9x/10 + k.
Which one of the follow ing must be true about line segments AO and BO ?
(A) AO > BO
(B) AO < BO
(C) AO < BO
(D) AO = BO
(E) AO = BO/2
Since y = 9x/10 + k is in slope-intercept form, we know the slope of
the line is 9/10. Now, the ratio of BO to AO is the slope of the line (rise
over run). Hence, BO/AO = 9/10. Multiplying both sides of this equation
by AO yields BO = 9AC/10. In other words, BO is 9/10 the length of AO.
Hence, AO is longer. The answer is (A).
INEQUALITIES
Inequalities are manipulated algebraically the same way as equations
with one exception:
Multiplying or dividing both sides of an inequality by a negative
number reverses the inequality. That is, if x > y and c < 0,
then cx < cy.
Example: For which values of x is 4x + 3 > 6x - 8?
As with equations, our goal is to isolate x on one side:
Subtracting 6x from both sides yields -2x + 3 > -8
Subtracting 3 from both sides yields -2x > -11
Dividing both sides by -2 and reversing the inequality yields
x < 11/2
Positive & Negative Numbers
A number greater than 0 is positive. On the number line, positive
numbers are to the right of 0. A number less than 0 is negative.
On the number line, negative numbers are to the left of 0. Zero
is the only number that is neither positive nor negative; it divides
the two sets of numbers. On the number line, numbers increase
to the right and decrease to the left.
The expression x > y means that x is greater than y. In other
words, x is to the right of y on the number line.
We usually have no trouble determining which of two numbers is
larger when both are positive or one is positive and the other
negative (e.g., 5 > 2 and 3.1 > -2). However, we sometimes hesitate
when both numbers are negative (e.g., -2 > -4.5). When in doubt,
think of the number line: if one number is to the right of another
number, then it is larger.
Miscellaneous Properties of Positive and Negative Numbers
1. The product (quotient) of positive numbers is positive.
2. The product (quotient) of a positive number and a negative
number is negative.
3. The product (quotient) of an even number of negative numbers
is positive.
4. The product (quotient) of an odd number of negative numbers
is negative.
5. The sum of negative numbers is negative.
6. A number raised to an even exponent is greater than or equal
to zero.
Absolute Value
The absolute value of a number is its distance on the number
line from 0. Since distance is a positive number, absolute value
of a number is positive. Two vertical bars denote the absolute
value of a number: | x |. For example, | 3 | = 3 and | -3 | =
3.
Students rarely struggle with the absolute value of numbers:
if the number is negative, simply make it positive; and if it
is already positive, leave it as is. For example, since -2.4 is
negative, | -2.4 | = 2.4 and since 5.01 is positive | 5.01 | =
5.01.
Further, students rarely struggle with the absolute value of
positive variables: if the variable is positive, simply drop the
absolute value symbol. For example, if x > 0, then | x | = x.
However, negative variables can cause students much consternation.
If x is negative, then | x | = -x. This often confuses students
because the absolute value is positive but the -x appears to be
negative. It is actually positive--it is the negative of a negative
number, which is positive. To see this more clearly let x = -k,
where k is a positive number. Then x is a negative number. So
| x | = -x = -(-k) = k. Since k is positive so is -x. Another
way to view this is | x | = -x = (-1)x = (-1)(a negative number)
= a positive number.
Transitive Property
If x < y and y < z, then x < z.
FRACTIONS
I. To compare two fractions, cross-multiply. The larger number
will be on the same side as the larger fraction.
Example:
| Column A |
Column B |
| 9/10 |
10/11 |
Cross-multiplying gives (9)(11) versus (10)(10), which reduces
to 99 versus 100. Now, 100 is greater than 99. Hence, 10/11 is
greater than 9/10.
III. To solve a fractional equation, multiply both sides by
the LCD (lowest common denominator) to clear fractions.
Example: If (x + 3)/(x - 3) = y, what is the value of
x in terms of y?
(A) 3 - y (B) 3/y (C) (2 + y)/(y - 2) (D) (-3y -3)/(1 - y) (E)
3y/2
First, multiply both sides of the equation by x - 3: (x - 3)(x
+ 3)/(x - 3) = (x - 3)y
Cancel the (x - 3's) on the left side of the equation: x + 3
= (x - 3)y
Distribute the y: x + 3 = xy - 3y
Subtract xy and 3 from both sides: x - xy = -3y - 3
Factor out the x on the left side of the equation: x(1 - y) =
-3y - 3
Finally, divide both sides of the equation by 1 - y: x = (-3y
-3)/(1 - y)
Hence, the answer is (D).
IV. When dividing a fraction by a whole number (or vice versa),
you must keep track of the main division bar.
Example: a/(b/c) = a(c/b) = ac/b. But (a/b)/c = (a/b)(1/c)
= a/(bc).
V. Two fractions can be added quickly by cross-multiplying:
a/b + c/d = (ad + bc)/bd
Example: 1/2 - 3/4 =
(A) -5/4 (B) -2/3 (C) -1/4 (D) 1/2 (E) 2/3
Cross multiplying the expression 1/2 - 3/4 yields [1(4) - 2(3)]/2(4)
= (4 - 6)/8 = -2/8 = -1/4. Hence, the answer is (C).
VI. To find a common denominator of a set of fractions, simply
double the largest denominator until all the other denominators
divide into it evenly.
VII. Fractions often behave in unusual ways: Squaring a fraction
makes it smaller, and taking the square root of a fraction makes
it larger. (Caution: This is true only for proper fractions,
that is, fractions between 0 and 1.)
Example: 1/3 squared equals 1/9 and 1/9 is less than 1/3.
Also the square root of 1/4 is 1/2 and 1/2 is greater than 1/4.
AVERAGES
Problems involving averages are very common on the SAT. They
can be classified into four major categories as follows.
I. The average of N numbers is their sum divided by N, that
is, average = sum/N.
Example: What is the average of x, 2x, and 6?
By the definition of an average, we get (x + 2x + 6)/3 = (3x
+ 6)/3 = 3(x + 2)/3 = x + 2.
II. Weighted average: The average between two sets of numbers
is closer to the set with more numbers.
Example: If on a test three people answered 90% of the
questions correctly and two people answered 80% correctly, then
the average for the group is not 85% but rather [3(90) + 2(80)]/5
= 430/5 = 86. Here, 90 has a weight of 3--it occurs 3 times. Whereas
80 has a weight of 2--it occurs 2 times. So the average is closer
to 90 than to 80 as we have just calculated.
III. Using an average to find a number.
Sometimes you will be asked to find a number by using a given
average. An example will illustrate.
Example: If the average of five numbers is -10, and the
sum of three of the numbers is 16, then what is the average of
the other two numbers?
(A) -33 (B) -1 (C) 5 (D) 20 (E) 25
Let the five numbers be a, b, c, d, e. Then their average is
(a + b + c + d + e)/5 = -10. Now three of the numbers have a sum
of 16, say, a + b + c = 16. So substitute 16 for a + b + c in
the average above: (16 + d + e)/5 = -10. Solving this equation
for d + e gives d + e = -66. Finally, dividing by 2 (to form the
average) gives (d + e)/2 = -33. Hence, the answer is (A).
IV. Average Speed = Total Distance/Total Time
Although the formula for average speed is simple, few people
solve these problems correctly because most fail to find both
the total distance and the total time.
Example: In traveling from city A to city B, John drove
for 1 hour at 50 mph and for 3 hours at 60 mph. What was his average
speed for the whole trip?
(A) 50 (B) 53 1/2 (C) 55 (D) 56 (E) 57 1/2
The total distance is 1(50) + 3(60) = 230. And the total time
is 4 hours. Hence, Average Speed = Total Distance/Total Time =
230/4 = 57 1/2. The answer is (E). Note, the answer is not the
mere average of 50 and 60. Rather the average is closer to 60
because he traveled longer at 60 mph (3 hrs) than at 50 mph (1
hr).
RATIO & PROPORTION
Ratio
A ratio is simply a fraction. Both of the following notations
express the ratio of x to y: x:y, x/y. A ratio compares two numbers.
Just as you cannot compare apples and oranges, so too must the
numbers you are comparing have the same units. For example, you
cannot form the ratio of 2 feet to 4 yards because the two numbers
are expressed in different units--feet vs. yards. It is quite
common for the SAT to ask for the ratio of two numbers with different
units. Before you form any ratio, make sure the two numbers are
expressed in the same units.
Example: What is the ratio of 2 feet to 4 yards?
The ratio cannot be formed until the numbers are expressed in the
same units. Let's turn the yards into feet. Since there are 3 feet in a
yard, 4 yards = 4 x 3 feet = 12 feet. Forming the ratio yields (2 feet)/(12
feet) = 1/6 or 1:6.
Proportion
A proportion is simply an equality between two ratios (fractions).
For example, the ratio of x to y is equal to the ratio of 3 to
2 is translated as x/y = 3/2. Two variables are directly proportional
if one is a constant multiple of the other:
y = kx, where k is a constant.
The above equation shows that as x increases (or decreases) so
does y. This simple concept has numerous applications in mathematics.
For example, in constant velocity problems, distance is directly
proportional to time: d = vt, where v is a constant. Note, sometimes
the word directly is suppressed.
Example: If the ratio of y to x is equal to 3 and the
sum of y and x is 80, what is the value of y?
(A) -10 (B) -2 (C) 5 (D) 20 (E) 60
Translating "the ratio of y to x is equal to 3" into an equation
yields: y/x = 3
Translating "the sum of y and x is 80" into an equation yields:
y + x = 80
Solving the first equation for y gives: y = 3x.
Substituting this into the second equation yields
3x + x = 80
4x = 80
x = 20
Hence, y = 3x = 3(20) = 60. The answer is (E).
In many word problems, as one quantity increases (decreases),
another quantity also increases (decreases). This type of problem
can be solved by setting up a direct proportion.
Example: If Biff can shape 3 surfboards in 50 minutes,
how many surfboards can he shape in 5 hours?
(A) 16 (B) 17 (C) 18 (D) 19 (E) 20
As time increases so does the number of shaped surfboards. Hence,
we set up a direct proportion. First, convert 5 hours into minutes:
5 hours = 5 x 60 minutes = 300 minutes. Next, let x be the number
of surfboards shaped in 5 hours. Finally, forming the proportion
yields
3/50 = x/300
3(300)/50 = x
18 = x
The answer is (C).
If one quantity increases (or decreases) while another quantity
decreases (or increases), the quantities are said to be inversely
proportional. The statement "y is inversely proportional to x"
is written as
y = k/x, where k is a constant.
Multiplying both sides of y = k/x by x yields
yx = k
Hence, in an inverse proportion, the product of the two quantities
is constant. Therefore, instead of setting ratios equal, we set
products equal.
In many word problems, as one quantity increases (decreases),
another quantity decreases (increases). This type of problem can
be solved by setting up a product of terms.
Example: If 7 workers can assemble a car in 8 hours, how
long would it take 12 workers to assemble the same car?
(A) 3hrs (B) 3 1/2hrs (C) 4 2/3hrs (D) 5hrs (E) 6 1/3hrs
As the number of workers increases, the amount time required
to assemble the car decreases. Hence, we set the products of the
terms equal. Let x be the time it takes the 12 workers to assemble
the car. Forming the equation yields
7(8) = 12x
56/12 = x
4 2/3 = x
The answer is (C).
To summarize: if one quantity increases (decreases) as another
quantity also increases (decreases), set ratios equal. If one
quantity increases (decreases) as another quantity decreases (increases),
set products equal.
EXPONENTS & ROOTS
Exponents
There are five rules that govern the behavior of exponents:
Problems involving these five rules are common on the SAT, and
they are often listed as hard problems. However, the process of
solving these problems is quite mechanical: simply apply the five
rules until they can no longer be applied.
Roots
There are only two rules for roots that you need to know for
the SAT:
FACTORING
To factor an algebraic expression is to rewrite it as a product
of two or more expressions, called factors. In general, any expression
on the SAT that can be factored should be factored, and any expression
that can be unfactored (multiplied out) should be unfactored.
Distributive Rule
The most basic type of factoring involves the distributive rule:
ax + ay = a(x + y)
For example, 3h + 3k = 3(h + k), and 5xy + 45x = 5xy + 9(5x)
= 5x(y + 9). The distributive rule can be generalized to any number
of terms. For three terms, it looks like ax + ay + az = a(x +
y + z). For example, 2x + 4y + 8 = 2x + 2(2y) + 2(4) = 2(x + 2y
+ 4).
Example: If x - y = 9, then (x - y/3) - (y - x/3) =
(A) -4 (B) -3 (C) 0 (D) 12 (E) 27
(x - y/3) - (y - x/3) =
x - y/3 - y + x/3 =
4x/3 - 4y/3 =
4(x - y)/3 =
4(9)/3 =
12
The answer is (D).
Difference of Squares
One of the most important formulas on the SAT is the difference
of squares:
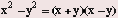
Example: If x does not equal -2, then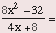
(A) 2(x - 2) (B) 2(x - 4) (C) 8(x + 2) (D) x - 2 (E) x + 4
In most algebraic expressions involving multiplication or division,
you won't actually multiply or divide, rather you will factor
and cancel, as in this problem.
2(x - 2)
The answer is (A).
Perfect Square Trinomials
Like the difference of squares formula, perfect square trinomial
formulas are very common on the SAT.
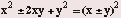
For example,
.
ALGEBRAIC EXPRESSIONS
A mathematical expression that contains a variable is called
an algebraic expression. Some examples of algebraic expressions
are 3x - 2y, 2z/y. Two algebraic expressions are called like terms
if both the variable parts and the exponents are identical. That
is, the only parts of the expressions that can differ are the
coefficients. For example, x + y and -7(x + y) are like terms.
However, x - y and 2 - y are not like terms.
Adding & Subtracting Algebraic Expressions
Only like terms may be added or subtracted. To add or subtract
like terms, merely add or subtract their coefficients:
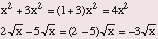
You may add or multiply algebraic expressions in any order. This
is called the commutative property:
x + y = y + x
xy = yx
For example, -2x + 5x = 5x + (-2x) = (5 - 2)x = -3x and (x -
y)(-3) = (-3)(x - y) = (-3)x - (-3)y = -3x + 3y.
Caution: the commutative property does not apply to division
or subtraction.
When adding or multiplying algebraic expressions, you may regroup
the terms. This is called the associative property:
x + (y + z) = (x + y) + z
x(yz) = (xy)z
Notice in these formulas that the variables have not been moved,
only the way they are grouped has changed: on the left side of
the formulas the last two variables are grouped together, and
on the right side of the formulas the first two variables are
grouped together.
For example, (x -2x) + 5x = (x + [-2x]) + 5x = x + (-2x + 5x)
= x + 3x = 4x and 24x = 2x(12x) = 2x(3x4x) = (2x3x)4x = 6x4x =
24x
Caution: the associative property doesn't apply to division or
subtraction.
Notice in the first example that we changed the subtraction into
negative addition: (x - 2x) = (x + [- 2x]). This allowed us to
apply the associative property over addition.
Parentheses
When simplifying expressions with nested parentheses, work from
the inner most parentheses out:
5x + (y - (2x - 3x)) = 5x + (y - (-x)) = 5x + (y + x) = 6x +
y
Sometimes when an expression involves several pairs of parentheses,
one or more pairs are written as brackets. This makes the expression
easier to read:
2x(1 -[y + 2(3 - y)]) =
2x(1 -[y + 6 - 2y]) =
2x(1 -[-y + 6]) =
2x(1 + y - 6) =
2x(y - 5) =
2xy - 10x
Order of Operations: (PEMDAS)
When simplifying algebraic expressions, perform operations within
parentheses first and then exponents and then multiplication and
then division and then addition and then subtraction. This can
be remembered by the mnemonic:
PEMDAS
Please Excuse My Dear Aunt
Sally
GRAPHS
Questions involving graphs rarely involve any significant calculating.
Usually, the solution is merely a matter of interpreting the graph.
1. During which year was the company's earnings 10 percent of
its sales?
(A) 85 (B) 86 (C) 87 (D) 88 (E) 90
Reading from the graph, we see that in 1985 the company's earnings
were $8 million and its sales were $80 million. This gives 8/80
= 1/10 = 10/100 = 10%. The answer is (A).
2. During what two-year period did the company's earnings increase
the greatest?
(A) 85-87 (B) 86-87 (C) 86-88 (D) 87-89 (E) 88-90
Reading from the graph, we see that the company's earnings increased
from $5 million in 1986 to $10 million in 1987, and then to $12
million in 1988. The two-year increase from '86 to '88 was $7
million--clearly the largest on the graph. The answer is (C).
3. During the years 1986 through 1988, what were the average
earnings per year?
(A) 6 million (B) 7.5 million (C) 9 million (D) 10 million (E)
27 million
The graph yields the following information:
| Year |
Earnings |
| 1986 |
$5 million |
| 1987 |
$10 million |
| 1988 |
$12 million |
Forming the average yields (5 + 10 + 12)/3 = 27/3 = 9. The answer
is (C).
4. If Consolidated Conglomerate's earnings are less than or equal
to 10 percent of sales during a year, then the stockholders must
take a dividend cut at the end of the year. In how many years
did the stockholders of Consolidated Conglomerate suffer a dividend
cut?
(A) None (B) One (C) Two (D) Three (E) Four
Calculating 10 percent of the sales for each year yields
| Year |
10% of Sales (millions) |
Earnings (millions) |
| 85 |
.10 x 80 = 8 |
8 |
| 86 |
.10 x 70 = 7 |
5 |
| 87 |
.10 x 50 = 5 |
10 |
| 88 |
10 x 80 = 8 |
12 |
| 89 |
.10 x 90 = 9 |
11 |
| 90 |
.10 x 100 = 10 |
8 |
Comparing the right columns shows that earnings were 10 percent
or less of sales in 1985, 1986, and 1990. The answer is (D).
WORD PROBLEMS
Although exact steps for solving word problems cannot be given,
the following guidelines will help:
(1) First, choose a variable to stand for the least unknown quantity,
and then try to write the other unknown quantities in terms of
that variable.
For example, suppose we are given that Sue's age is 5 years less
than twice Jane's and the sum of their ages is 16. Then Jane's
age would be the least unknown, and we let x = Jane's age. Expressing
Sue's age in terms of x gives Sue's age = 2x - 5.
(2) Second, write an equation that involves the expressions in
Step 1. Most (though not all) word problems pivot on the fact
that two quantities in the problem are equal. Deciding which two
quantities should be set equal is usually the hardest part in
solving a word problem since it can require considerable ingenuity
to discover which expressions are equal.
For the example above, we would get (2x - 5) + x = 16.
(3) Third, solve the equation in Step 2 and interpret the result.
For the example above, we would get by adding the x's: 3x - 5
= 16. Then adding 5 to both sides gives 3x = 21. Finally, dividing
by 3 gives x = 7. Hence, Jane is 7 years old and Sue is 2x - 5
= 2(7) - 5 = 9 years old.
Motion Problems
Virtually, all motion problems involve the formula Distance =
Rate x Time, or
D = R x T
Example : Scott starts jogging from point X to point Y.
A half-hour later his friend Garrett who jogs 1 mile per hour
slower than twice Scott's rate starts from the same point and
follows the same path. If Garrett overtakes Scott in 2 hours,
how many miles will Garrett have covered?
(A) 2 1/5 (B) 3 1/3 (C) 4 (D) 6 (E) 6 2/3
Following Guideline 1, we let r = Scott's rate. Then 2r - 1 =
Garrett's rate. Turning to Guideline 2, we look for two quantities
that are equal to each other. When Garrett overtakes Scott, they
will have traveled the same distance. Now, from the formula D
= R x T, Scott's distance is D = r x 2 1/2 and Garrett's distance
is D = (2r - 1)2 = 4r - 2. Setting these expressions equal to
each other gives 4r - 2 = r x 2 1/2. Solving this equation for
r gives r = 4/3. Hence, Garrett will have traveled D = 4r - 2
= 4(4/3) - 2 = 3 1/3 miles. The answer is (B).
Work Problems
The formula for work problems is Work = Rate x Time, or W = R
x T. The amount of work done is usually 1 unit. Hence, the formula
becomes 1 = R x T. Solving this for R gives R = 1/T.
Example : If Johnny can mow the lawn in 30 minutes and
with the help of his brother, Bobby, they can mow the lawn 20
minutes, how long would take Bobby working alone to mow the lawn?
(A) 1/2 hour (B) 3/4 hour (C) 1 hour (D) 3/2 hours (E) 2 hours
Let r = 1/t be Bobby's rate. Now, the rate at which they work
together is merely the sum of their rates:
Total Rate = Johnny's Rate + Bobby's Rate
1/20 = 1/30 + 1/t
1/20 - 1/30 = 1/t
(30 - 20)/(30)(20) = 1/t
1/60 = 1/t
t = 60
Hence, working alone, Bobby can do the job in 1 hour. The answer
is (C).
Mixture Problems
The key to these problems is that the combined total of the concentrations
in the two parts must be the same as the whole mixture.
Example : How many ounces of a solution that is 30 percent
salt must be added to a 50-ounce solution that is 10 percent salt
so that the resulting solution is 20 percent salt?
(A) 20 (B) 30 (C) 40 (D) 50 (E) 60
Let x be the ounces of the 30 percent solution. Then 30%x is
the amount of salt in that solution. The final solution will be
50 + x ounces, and its concentration of salt will be 20%(50 +
x). The original amount of salt in the solution is 10%(50). Now,
the concentration of salt in the original solution plus the concentration
of salt in the added solution must equal the concentration of
salt in the resulting solution: 10%(50) + 30%x = 20%(50 + x).
Multiply this equation by 100 to clear the percent symbol and
then solving for x yields x = 50. The answer is (D).
Coin Problems
The key to these problems is to keep the quantity of coins distinct
from the value of the coins. An example will illustrate.
Example : Laura has 20 coins consisting of quarters and
dimes. If she has a total of $3.05, how many dimes does she have?
(A) 3 (B) 7 (C) 10 (D) 13 (E) 16
Let D stand for the number of dimes, and let Q stand for the
number of quarters. Since the total number of coins in 20, we
get D + Q = 20, or Q = 20 - D. Now, each dime is worth 10 cents,
so the value of the dimes is 10D. Similarly, the value of the
quarters is 25Q = 25(20 - D). Summarizing this information in
a table yields
| |
Dimes |
Quarters |
Total |
| Number |
D |
20 - D |
20 |
| Value |
10D |
25(20 - D) |
305 |
Notice that the total value entry in the table was converted
from $3.05 to 305 cents. Adding up the value of the dimes and
the quarters yields the following equation:
10D + 25(20 - D) = 305
10D + 500 - 25D = 305
-15D = -195
D = 13
Hence, there are 13 dimes, and the answer is (D).
Age Problems
Typically, in these problems, we start by letting x be a person's
current age and then the person's age a years ago will be x -
a and the person's age a years in future will be x + a. An example
will illustrate.
Example : John is 20 years older than Steve. In 10 years,
Steve's age will be half that of John's. What is Steve's age?
(A) 2 (B) 8 (C) 10 (D) 20 (E) 25
Steve's age is the most unknown quantity. So we let x = Steve's
age and then x + 20 is John's age. Ten years from now, Steve and
John's ages will be x + 10 and x + 30, respectively. Summarizing
this information in a table yields
| |
Age now |
Age in 10 years |
| Steve |
x |
x + 10 |
| John |
x + 20 |
x + 30 |
Since "in 10 years, Steve's age will be half that of John's,"
we get
(x + 30)/2 = x + 10
x + 30 = 2(x + 10)
x + 30 = 2x + 20
x = 10
Hence, Steve is 10 years old, and the answer is (C).
