GRE Math - Factoring Review
Click the links immediately below to view the other GRE diagnostic tests.
Verbal Test
FACTORING
To factor an algebraic expression is to rewrite it as a product of two or more expressions, called factors. In general, any expression on the GRE that can be factored should be factored, and any expression that can be unfactored (multiplied out) should be unfactored.
Distributive Rule
The most basic type of factoring involves the distributive rule:
ax + ay = a(x + y)
For example, 3h + 3k = 3(h + k), and 5xy + 45x = 5xy + 9(5x) = 5x(y + 9). The distributive rule can be generalized to any number of terms. For three terms, it looks like
ax + ay + az = a(x + y + z)
For example, 2x + 4y + 8 = 2x + 2(2y) + 2(4) = 2(x + 2y + 4).
Example: If x - y = 9, then (x - y/3) - (y - x/3) =
(A) -4 (B) -3 (C) 0 (D) 12 (E) 27
(x - y/3) - (y - x/3) =
x - y/3 - y + x/3 =
4x/3 - 4y/3 =
4(x - y)/3 =
4(9)/3 =
12
The answer is (D).
Difference of Squares
One of the most important formulas on the GRE is the difference of squares:
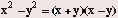
Example: If x does not equal -2, then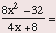
(A) 2(x - 2) (B) 2(x - 4) (C) 8(x + 2) (D) x - 2 (E) x + 4
In most algebraic expressions involving multiplication or division, you won't actually
multiply or divide, rather you will factor and cancel, as in this problem.
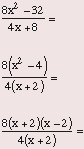
2(x - 2)
The answer is (A).
|

